Video quality measurement has been gaining more attention. Video service providers, television network operators, surveillance equipment manufacturers and broadcasters need to ensure that the video products and services they offer meet minimum quality requirements. Although the network bandwidth has been increased but higher and higher resolution of video is being carried over limited bandwidths. There are several video quality metrics including PSNR, VQM, MPQM, SSIM and NQM.

PSNR

PSNR is derived by setting the mean squared error (MSE) in relation to the maximum possible value of the luminance as follows:

$\mathit{MSE} = \frac{1}{m\,n}\sum_{i=0}^{m-1}\sum_{j=0}^{n-1} [I(i,j) - K(i,j)]^2$

$\begin{align}\mathit{PSNR} &= 10 \cdot \log_{10} \left( \frac{\mathit{MAX}_I^2}{\mathit{MSE}} \right)\\ &= 20 \cdot \log_{10} \left( \frac{\mathit{MAX}_I}{\sqrt{\mathit{MSE}}} \right)\end{align}$

Where f(i,j) is the original signal at pixel (i, j), F(i, j) is the reconstructed signal, and M x N is the picture size. The result is a single number in decibels, ranging from 30 to 40 for medium to high quality video.

Despite several objective video quality models have been developed in the past two decades, PSNR continues to be the most popular evaluation of the quality difference among pictures.

Video Quality Metric (VQM)

VQM is developed by ITS to provide an objective measurement for perceived video quality. It measures the perceptual effects of video impairments including blurring, jerky/unnatural motion, global noise, block distortion and color distortion, and combines them into a single metric. The testing results show VQM has a high correlation with subjective video quality assessment and has been adopted by ANSI as an objective video quality standard.

Moving Pictures Quality Metric (MPQM)

MPQM is an objective quality metric for moving picture which incorporates two human vision characteristics as mentioned above. It first decomposes an original sequence and a distorted version of it into perceptual channels. A channel-based distortion measure is then computed, accounting for contrast sensitivity and masking. Finally, the data is pooled over all the channels to compute the quality rating which is then scaled from 1 to 5 (from bad to excellent).

The actual computation of the distortion E for a given block is given by

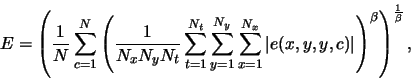
$\begin{displaymath}E= \left (\frac {1}{N} \sum_{c=1}^N \left( \frac{1}{N_x N_y... ...x,y,y,c)\right\vert \right)^\beta \right)^{\frac{1}{\beta}}, \end{displaymath}$

where

is the masked error signal at position

and time

in the current block and in the channel

;

and

are the horizontal and vertical dimensions of the blocks;

is the number of channels. $\beta$ is a constant having the value 4. The final quality measure can be expressed either using the Masked PSNR (MPSNR) as follows

$\begin{displaymath}MPSNR=10\log\frac{255^2}{E^2}, \end{displaymath}$

or can be mapped to the 5-point ITU quality scale using the equation

$\begin{displaymath}Q=\frac{5}{1+ \ \gamma E},\end{displaymath}$

where $\gamma$ is a constant to be obtained experimentally. This can be done if the subjective quality rating

is known for a given sequence,

has to be computed and then one solves for $\gamma$ from the last equation.

Structural Similarity Index (SSIM)

SSIM uses the structural distortion measurement since the human vision system is highly specialized in extracting structural information from the viewing field and it is not specialized in extracting the errors.

If you let x = {x_i | i = 1,2,…,N} be the original signal and y = {y_i| i = 1,2,…,N} be the distorted signal the structural similarity index can be calculated as:

$SSIM(x,y) = \frac{(2\mu_x\mu_y + c_1)(2\sigma_{xy} + c_2)}{(\mu_x^2 + \mu_y^2 + c_1)(\sigma_x^2 + \sigma_y^2 + c_2)}$

with

$\scriptstyle\mu_x$ the average of $\scriptstyle x$ ;
$\scriptstyle\mu_y$ the average of $\scriptstyle y$ ;
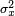$\scriptstyle\sigma_x^2$ the variance of $\scriptstyle x$ ;
$\scriptstyle\sigma_y^2$ the variance of $\scriptstyle y$ ;
$\scriptstyle \sigma_{xy}$ the covariance of $\scriptstyle x$ and $\scriptstyle y$ ;
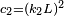$\scriptstyle c_1 = (k_1L)^2$ , $\scriptstyle c_2 = (k_2L)^2$ two variables to stabilize the division with weak denominator;
$\scriptstyle L$ the dynamic range of the pixel-values (typically this is $\scriptstyle 2^{\#bits\ per\ pixel}-1$ );
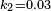$\scriptstyle k_1 = 0.01$ and $\scriptstyle k_2 = 0.03$ by default.

Noise Quality Measure (NQM)

In NQM, a degraded image is modeled as an original image that has been modeled as an original image that has been subjective to linear frequency distortion and additive noise injection. These two sources of degradation are considered independent and are decoupled into two quality measures: a distortion measure (DM) of the effect of frequency distortion, and a noise quality measure (NQM) of the effect of additive noise. The NQM takes into account : (1) variation in contrast sensitivity with distance, image dimensions; (2) variation in the local luminance mean; (3) contrast interaction between spatial frequencies; (4) contrast masking effects. The DM is computed in three steps. First, the frequency distortion in the degraded image is found. Second, the deviation of this frequency distortion from an all-pass response unity gain is computed. Finally, the deviation is weighted by a model of the frequency response of the human visual system.

HDfpga

Friday, February 19, 2010

Video Quality Measurement Metrics

PSNR

Video Quality Metric (VQM)

Moving Pictures Quality Metric (MPQM)

Structural Similarity Index (SSIM)

No comments:

Followers

Blog Archive

About Me